分类问题中Sigmoid-与-Softmax-区别
作者:数据人阿多
背景
利用神经网络进行分类任务时,在最后需要经过激活函数,对神经网络的原始输出值进行处理,输出每个类别的概率。本文将讨论用Sigmoid函数或Softmax函数处理原始输出值,进行分类问题。
Sigmoid函数
公式如下所示:
$$s(x_i)=\frac{1}{1+ e^{-x_i}}$$
函数曲线,单调递增,并且值域(0,1):
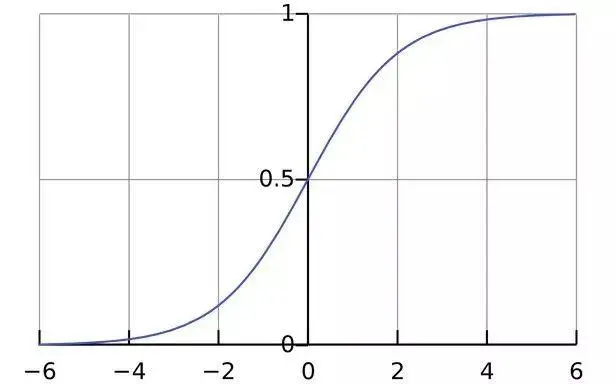
可以看出对于每个值 $[x_1,x_2,x_3,...,x_n]$,都能计算出其对应的Sigmoid函数值,他们之间互不影响,只和 $x_i$ 大小有关
以上为纯数学理论,回到神经网络分类问题,神经网络的原始输出值,经过Sigmoid函数后,可以计算出各个类别的概率,那么这些概率之间互不影响,他们之和有可能大于1,有可能小于1。
由于各个类别概率相互独立,Sigmoid函数可以用于多分类任务问题,比如一张图片里面,既有狗也有猫也有人,那么神经网络训练后,输出的原始值,经过Sigmoid函数,狗、猫、人的概率应该都比较高且接近于1
Softmax函数
公式如下所示: $$s(x_i)=\frac{e^{x_i}}{e^{x_1}+e^{x_2}+...+e^{x_n}}$$ 通过公式可以看出每个值 $[x_1,x_2,x_3,...,x_n]$,经过Softmax函数后,所有输出概率的总和为1,类似与标准化概念,由于分母是所有值经过计算后的和,所以求出的概率不是相互独立,而是有关的,也就是有概率大的,那么就有概率小的,总之他们的和为1
回到神经网络,神经网络输出的原始值,经过Softmax函数,可以计算出各个类别的概率,且各类别的概率之和为1
由于各个类别概率不是相互独立,概率之和为1,Softmax函数常用于二分类任务问题,比如NLP的情感判别问题,那么神经网络训练后,输出的原始值,经过Softmax函数,正向与负向的概率和为1,那么肯定有一个概率大于0.5,一个概率小于0.5,可以用来判断一个句子的正负向
区别
- Sigmoid函数
Sigmoid =多类别分类问题=可以有多个正确答案=独立输出
例如:图像里面包含多个物体
- Softmax函数
Softmax =多类别分类问题=只有一个正确答案=非相互独立
例如:手写数字
常用于二分类问题
历史相关文章
以上是自己实践中遇到的一些问题,分享出来供大家参考学习,欢迎关注微信公众号DataShare,不定期分享干货